上次我们说到了如何用键盘操作Google搜索，这次我们要介绍的是一个网站。如果你是dos / Linux / FreeBSD等console based操作系统的死忠的话，你一定会爱上这个网站的：goosh.org提供命令行形式的Google搜索，你可以搜索的内容包括网页，新闻，feed，blog，地图，图片，视频……甚至还可以在这个界面查看Gmail信箱！
进入goosh.org后h回车可查看命令帮助。
注意：本文保留所有权利。基于下述实验方法发文章的话，要和我联系，根据文章的实验目的，我可能要求作为第一或者第二至第N作者。如果出于非商业和非科研的目的，您可以自由利用文中的方法和程序。
基本原理：猫是好奇的动物，本能会追逐移动的物体。利用计算机产生一个条纹图形，它的对比度和空间频率已知，然 后放置在一个背景色块之上移动，背景色块的颜色是前景色的平均值。如果猫能够看到，那么就会有追逐行为发生，反之则没有。为了一开始吸引猫咪的注意力，前 景条纹还要在一个背景色明显不同的地方先移动一下。
第一步：产生前景和背景图片：
下面是Matlab程序，用来产生前景条纹和背景色块。
clear all; close all
% 清理工作区
w=200;% 产生一个长宽都是200个像素的图片
k=72; % 空间频率,这里是在200个像素的长度里面,有k个周期，实际的定义需要根据具体显示器的大小而定,
n=256^2*1/3
% 65536是屏幕的最大亮度,也就是全白
% n定义的是亮度的最高值,这个数值可以定义对比度
alpha=135;%条纹旋转的角度，你可以检查猫咪各个角度的对比敏感度
a=ones(w,1); % 产生一个单位矩阵
dx=2kpi/w; % 每一个像素所需要的变化值
b=[0:dx:2kpi-dx];% 从0到2kpi,每个点均匀变化
c=(sin(b)+1)/2;% 产生正弦曲线,并且平移到x轴以上
d=c.*n;% 纵向放大正弦曲线
e=a*d; % 将正弦曲线扩展成平面
e=uint16(e); % 转化成16位整型整数
e=256^2-e; % 黑白颠倒一下
backgrounds=uint16(ones(600,800).mean2(e));% 产生一个800600大小的背景色块
e=imrotate(e,alpha,’bicubic’,'crop’); %把前景条纹旋转成指定的角度
e=e(50:150,50:150); %旋转以后周围会有黑边，所以只取中间的部分。
imwrite(backgrounds,’b1.tif’,'tif’);% 保存背景图片，文件名称是b1.tif
imwrite(e,’e1.tif’,'tif’); %保存前景图片，文件名是e1.tif
figure(1), imshow(e); %显示前景图片。
第二步：
建立一个空白的演示文稿，PC上用PPT，Mac上用keynote，Linux上用Open Office。不失一般性，以Keynote为例。
建立空白演示文稿。大小是1024768，将背景色块和前景色块插入。因为我们建立的背景色块是800600，所以有一部分空白的区域。注意，前景色块是在背景色块之上的。
创建一个动画，让前景色块首先在空白区域上移动，然后以另一种运动方式在背景色块上移动，比如在空白区域上先水平移动几次，然后进入背景色块，进行垂直运动。
第三步：
重复第一步。选择其他的对比度和空间频率。重复第二步，复制第一张幻灯，但是选择新建的前景图像与背景图像。
根据需要测量的需要来选择对比度和空间频率。
第四步：测量
首先要对显示器的屏幕进行测光，找一个全白的图片，测量显示器9宫格位置上的亮度，平均，三次。找一张全黑的图片，再测。分别获得显示器最亮和最暗 的照度。分别对应的是65536的灰度值和0的灰度值，不妨假设灰度值和亮度是线性关系，当然最好也验证一下。总之，对比度的计算方法就是条纹图形中＝ (max-min)/(max+min)
空间频率需要和显示器相对应，比如12寸4:3的笔记本，显示分辨率设定为1024768，那么水平或垂直两点的距离，就是12(英寸)25.4(mm/英寸)/54/1024=0.238mm。那么200个像素含有k个周期，就意味着空间频率＝k/(2000.238)(mm-1)线。注意，同时需要设定猫的测量距离。这个可以用一个玻璃罩子来控制猫到显示器之间的距离。要再利用这个距离算一下线数与角度之间的对应关系。把mm-1的单位转换成cycle/degree的单位。
测量时，将猫咪放再玻璃罩前，播放演示文稿。如果猫咪出现了追随运动，则认为它可以看见，否则则不能。
注意测量时候的背景光。推荐使用全黑的暗环境。
结果：进宝的测试录像，录像中，进宝的点头动作表明它可以看见前景条纹在背景中的移动：http://hellotxt.com/v/mhS
讨论：
首先，基于上述实验方法发文章的话，要和我联系，根据文章的实验目的，我可能要求作为第一或者第二至第N作者。
猫眼看似很强大，其实视力很差，据先贤们的在体和离体实验（faint，还有离体），猫的视力大概在5.5 c/d一下。人类正常的视力是1.0，也就是1′的视角，也就是1度的范围内有30次黑白重复的条纹，即30 c/d，按照我国的视力表，猫也就大概是0.1到0.2的视力吧。另外，猫没有红色的视锥细胞。所以只能分辨绿色、黄色和蓝色的组合。
由于猫的瞳孔不是圆形的，在亮环境下，其实各个方向的成像质量并不相同，如果要严格起见，一是应该在暗环境下测量，另一可以考虑散瞳。
致谢：
感谢进宝同学的加盟演出。
参考：
关于对比敏感度的基本知识，参考：讲课：调制传递函数- 金色葡萄的国内精华区
Matlab文件，keynote演示文稿，和已经做好的各个角度的条纹图像打包：http://goldengrape.org/?attachment_id=1589
One important update about the GoogleReader + Twitter” script. Including:
20081208- update the script fixing the firefox2 compitable problem and the bug in "list" mode
20081206- update the script when new GoogleReader update (4th Dec 08) has broken this script
This version uses the new UI same with Email function in GoogleReader.
When reading articles in GoogleReader, how to share the nice articles to Twitter at a rapid? I made one GreaseMonkey script for that, and you can now.
The format of messages
[Tag] Title(Note) URL
The basic function
The installation order
i. Install the browser - firefox
http://www.mozilla.com/en-US/
ii. Install the plugin - GreaseMonkey
http://addons.mozilla.org/en-US/firefox/addon/748
iii. Install this script
http://userscripts.org/scripts/show/10169
The specification
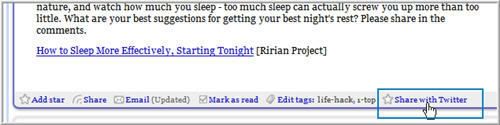
1. the link “Share with twitter”
After installing the script, open GoogleReader. Below each article, one link “Share with twitter” is added in the toolbar.
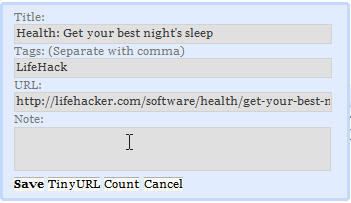
2. one mini window
Click the link, one mini window will popup. There are four inputboxes: Title, Tags, URL, and Note. Tag\title\URL are received from articles in GoogleReader automatically. And you can edit them. If you want to talk about it yourself, please input in “Note”.
3. four buttons
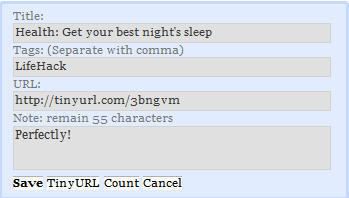
4. the user authentication
When you send the first message, one authentication is required. Please use your registered username or email address as the username component.
5. show the messages shared
You can install the script here:
http://userscripts.org/scripts/show/10169
来自friendlyatheist.com的一个邪恶的笑话，它告诉我们，在讲课之前先自己排演一遍有多么重要。
老师：同学们，这是一个什么形状啊？
学生：（齐声）四棱锥！
老师：很好！那它的展开图是什么样子呢（同时展开教具）？
学生：一个正方形和四个三角形！
老师：很好！那这个又是什么形状呀？
学生：（齐声）六棱柱！
老师：很好！那它的展开图又是什么样子呢（同时展开教具）？
学生：（大笑不停）
老师：……
让我们简单的回顾一下，美国人简单的一生，如大家常说的那样，因为制度优越导致外国人太过简单，头脑简单，经历看似复杂实则简单，只有像我们这样，生活在一个奇异制度下长达数千年的物种，才会一代又一代的『上下求索』怀疑人生。别人用来享受人生的时间，我们统统用来怀疑，所以我们是何等深沉的民族呀。
在美国，这个年轻的国家里，一个小孩从小接受基督教的熏陶（或者其它宗教的教育），民主自由观念的洗礼，长大后经历一下摇滚、大麻、左派、社会主义的洗礼，跟着就开始规规矩矩的生活，从宗教中获得此后人生的一切满足感，变得保守，虔诚的要命。
即便在困难时期，他们也生活优渥，几乎从无冻馁之患，不明白因制度带来的人间惨剧究竟是怎么一回事儿，事实上，无论历史中还是电影里，你很难看到美国电影将问题指向社会制度，他们最擅长诉诸个人的精神世界，就算探讨文化对社会的影响，也仅仅限于一个家庭之中，例如《American beauty》
《革命之路》也是此类探索型电影。
爱波和弗兰克的悲剧也是美国中产普遍的悲剧之一，它来自对自身精神世界的探索，对人生意义虚无的上穷碧落下黄泉。故事的结局，弗兰克在爱波的感召下，满怀激情的探索之后发现自己内心一片荒芜，其实，他一直都不愿承认，作为一个小职员，他挺享受这种『身边有个好看的，家里有个做饭的』感情和生活，而充满人生理想的爱波，不得不面对『嫁错郎』的惩罚，虽就死（我觉得堕胎在美国有着宗教上的意义）仍不悔，故事的结局之一，弗兰克眼神空洞的望着两个失去母亲的天真浪漫的小孩儿---他是不是在想，孩子们，你们现在很开心，长大后，生活不过如此啊，又过十几秒钟，镜头切向那一对儿革命路上的老夫妇，老太太饱含深情的摸着怀里的猫猫，对着老头絮絮叨叨谈起那一对儿曾经与众不同的夫妇，老头放下手中的报纸，缓缓的拿下助听器--用中国的话说，黄土埋到脖子了，他不愿再忍受，画面就此定格。
爱波夫妇（确切的说应该是爱波本人）以一己之力，凭一张在巴黎的旧照片发起的对未来的探险，对打破生活设置的努力，以悲惨的失败告终了。爱波夫妇闹出的动静，几乎令每个家庭都感到了危机，弗兰克的好同事，在一次家庭聚会上，忽然动感情的跑到后院儿，双手捏在一起低着头站着发呆，老婆追出来，他可怜的说：以后不要提弗兰克夫妇了，好吗？说实话我最鄙视的就是这位，他胆敢在车上和爱波做爱，面对自己的危机却选择了龟缩，小镇的生活也逐渐恢复平静，更荒谬的是，透过华丽的面纱，揭示生活本质的人，竟然是个精神病患者。在一次家庭聚会的歇斯底里中，他指着爱波的肚子说：我很庆幸我不是你腹中之婴，不必降生到这个世界（我怀疑，就是这个情景，令爱波最终决定自己堕胎）
片中的场景，大部分是蓝天白云，绿草树荫，西装礼帽，一栋栋绿树掩映百花盛开的小院落，展示了一副所谓太平盛世下一群衣冠楚楚的中产们貌似快乐安静的生活，但偶尔露出的几个画面，才叫惊心动魄，几乎可算是中年丑态百出图，中年男人微微隆起的腹部，女人松松垮垮的皮肤及掩盖不住的鱼尾纹，每日单调的日出日落，锅碗瓢盆.....最可怕的是日益封闭的内心和枯萎的灵魂，比如Milly太太，就算想一下有人居然胆敢告别如今的生活都能把自己吓的大哭，导演还算厚道，他故意弱化了孩子的情节，片中的夫妇们，都是儿女成双的家庭，却鲜有孩子出现，小孩的形象在这部电影里像是无足轻重的纸片儿--因为孩子并不是危机的原因。
作为一个以探求生活多样化为生活目标的爱波，最长出现的场景是不停的神经质的抽烟和流泪，泪水花了她已不再年轻的脸，她如此的与众不同，这种勇气和理想令她在舞会上熠熠闪光，在小镇上被人传说一时，她热情洋溢的对生活的不同可能性进行了探求，用生命完成了对模式化生活的抗拒。
世俗力量是如此巨大，在地球上任何一个地方都如是，从这个意义上讲，地球处处充满了一个个的现代化程度发展不同的猪圈，用力突破围墙固然可精神可嘉，但如果不够强大，操作不好，就会头破血流，接着回去过旧的生活，甚至再也回不去了，就此毁灭。如王小波笔下那头特立独行的猪兄一样，对生活的设置不屑一顾并能成功逃脱者，几乎只存在于想象当中，更何况，爱波想要突破的生活已经是一个完整的家庭的生活，不再是她一人的理想可以承载的。
探寻人生意义是种可怕的冒险，因为并非每一个躯壳里都装有一个灵魂，尽管美国的小孩，受到优越的教育，年轻时又有Graduation GAP可以到处去游历，见识天下的美景和美女，大学时能感受多元思想带来的冲击，可这不代表他们就能明白人生的意义，有足够的能力解决生活中的精神危机，如我们所见，进入生活，逐渐成长，不也一样是这个破德行？
我们可以略感欣慰的是，这样的危机不会在中国产生，中国已过中年，尚无中产，中国古训所谓：虚其心而实其腹，真是颠扑不破的真理，用某领导人的话说：『吃饱了没事儿干的人×××××』，连罗素都说：为下一餐而担忧的人，没有心理危机，中国一直生活在生存恐惧中，一代代的人都未曾逃脱饥饿恐惧，《活着》这样的小说已经成功的揭示了生活的全部意义生活的伟大成就就是：活着。所以，我们可能很难理解，你丫住着高尚社区的小别墅，后院有花有草，门口还有个小树林，家里有车，儿女双全，老公又有工作，你还想什么呢？目前我们每天兴高采烈孜孜以求的不过如此而已。
大约在我10-15岁之间，有一天，我到地里干活，经过大陆时，有一两四轮拖拉机扬起阵阵黄土，绝尘而去，黄土飘扬之中，我看到开拖拉机的小伙着一个落满尘土的棕色皮夹克，头发卷在一起微微抖动，他叼着烟卷儿，神气活现，轮子上的挡板上坐着他老婆，扶着老公的后背，颠簸之中，坐的稳稳当当，头巾飘飘，自信满满，幸福自豪之情溢于言表，他们哒哒哒哒的风驰电掣般呼啸而过，在那一刻我就想，这就是爱情和生活的全部意义所在呀 ，普天之下，莫不如是；二十年过去了，美国人民在寻死觅活于中产危机，而爱情和生活之于我们仍然如此，只是宝马奔驰代替了拖拉机，副驾上的小三代替了原配而已。
所以，我们没有如此指向内心的中产危机，因为中国根本没有一个叫做中产阶级的群体。中国亦没有此类型的电影作品，看看《手机》《一声叹息》就知道，所谓危机不过如此啊。
上次说到维度时，有人提到了如何理解四维空间的问题。这是一个非常有趣的话题，可是我一直没有用心写一下。前段时间网上出了一部片子叫做Dimensions: a walk through mathematics，据称里面详细介绍了四维空间。我本以为推荐一下这个片子就能少写一篇又臭又长的日志了的，没想到下下来看了之后发现该片奇差，不了解四维空间的人看了半天估计还是不了解四维空间。最近放假比较闲，打算慢慢来扯一下。如果你以前从来没细想过四维空间的话，相信今天你会有一种超凡脱俗的感觉。
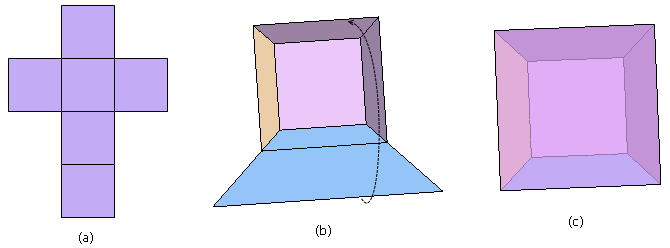
现在，假设我是一个二维世界的人，我不能理解什么是“高度”，什么是“体”，什么是“空间”。你想向我描述三维世界中的立方体。你该怎么说呢？你或许会从立方体的展开图开始谈起：图(a)就是一个立方体的展开图，如果我们剪一个这种形状的纸板，我们可以把它折成一个正方体。我开始好奇了。
- 你说说该怎么做呢？
- 先把上面几个正方形折起来，把对应的边粘在一起……
- 等会儿呢等会儿呢，这几个正方形是稳定的形状呀，它们的边怎么可能挨到一起呢？
- 傻了吧！在二维世界中它们不是活动的，但是它们可以向第三维度弯折啊！给你画一个图(b)吧，这就是把上面那几个正方形粘合起来的样子，这就成了一个没有封顶、还差一面的正方体……
- 你耍赖！你这样弯折了之后正方形都不是正方形了，都变成梯形了！
- 不对，它们仍然是正方形。图(b)的六块区域其实都是正方形，只是由于透视作用，它们看上去好像变“斜”了。
- 嗯，好吧，你继续。
- 现在我们得到的是一个有盖的盒子。上面五个正方形（其中有四个由于处于第三维度而变了形）的“内部”已经形成了“空间”了，可以往里面放东西了。要想做成一个封闭的正方体，只需要把剩下的那个正方形合上去就行了，最终结果就像图(c)那样。
- 咦？图(c)里面，刚才最后要合上去的那个正方形到哪儿去了？
- 它就是最大的那个正方形。
- 胡说！那个大正方形是五个小正方形拼成的！这个大正方形刚才在图(b)里也有！
- 不是的。图(b)里的大正方形的确是五个小正方形拼成的轮廓，但图(c)里的那个大正方形是真实存在的，它就是最后合上去的那一块。这个大正方形也并不是和那五个小正方形重叠在一起，它们在第三维中的层次是不同的。图(c)就是你梦想的那个正方体了，它由六个正方形组成。你在图(c)中看到的一个小正方形，一个大正方形，四个梯形事实上都是正方形，而且它们都一样大。这六个正方形围成了中间的那个“空间”。
- 我还是不明白。那个大正方形也是在第三维度的，为什么它没变形呢？
- 这是因为，这个正方形所在的方向不是第三个维度，因此看上去和原来一样。
- 那同一个方向上为什么又有一大一小两个正方形呢？
- 唉，真麻烦。这是因为，它们的朝向虽然一样，但在第三维度上的位置不一样。小的那个正方形在第三个维度离我们远一些，看起来就要小一些。
- 哦！我有点明白了。是不是说，旁边一圈那四个“正方形”是跨越了第三维的，因此在第三维空间中一部分离我们近，一部分离我们远，于是看上去就是由大到小渐变过去的，就像是变形了。
- 对！你理解得很好！说真的，平时生活在三维空间中，我都还没仔细想过这一点呢。
- 我好像真的明白了，说错了不要笑我哦。那个“空间”啊，说穿了就是大正方形擦着四个变形正方形在第三维度上向远处的小正方形移动所产生的“轨迹”。
- 正是正是！
- 哎呀我彻底明白了。怪不得我们说n维立方体有2^n个点呢，其实道理很简单。其实只需要把n-1维立方体复制一份，然后对应的顶点相连就可以了。这就是n-1维立方体在第n维发生位移的结果，新增的那2^(n-1)条边就是点的轨迹。
- 哎呀，你太他妈牛B了，读中文系真他妈可惜了。我还给你看一个好玩的东西，让你看看三维立方体是如何旋转的。睁大眼睛仔细看好每个正方形都变到哪儿去了。
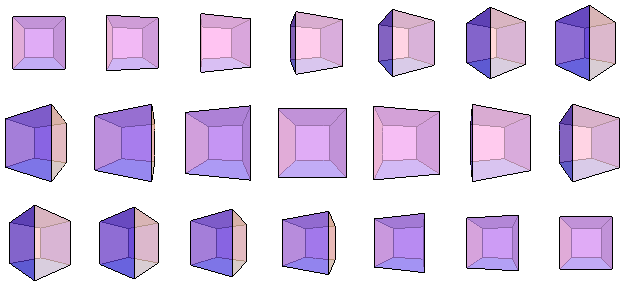
- 我又糊涂了。为什么从第三幅图变成第四幅图时，远处的小正方形能够穿越左边界，让其中一小半跑到边界左边来？
- 这个确实不好理解。小正方形并没有“穿过”那条竖直的边，那条边在第三维上离我们更近，而它在我们这个方向上的投影又与小正方形重合了。其实你可以看到，它们之间的拓扑关系仍然是不变的。
- 哦，于是乎远处的小正方形就转到侧面去了，然后又转到离我们近的位置来了，替代了原先大正方形的位置……
- 回去没事多想想吧。期待你睡觉时能够做出一个三维的梦。
- 好的。谢了。
好了，现在呢，告诉大家一个秘密，其实我是来自四维空间的人，很多人问我四维立方体是啥样子的，烦死我了，于是写下了今天的这篇日志。
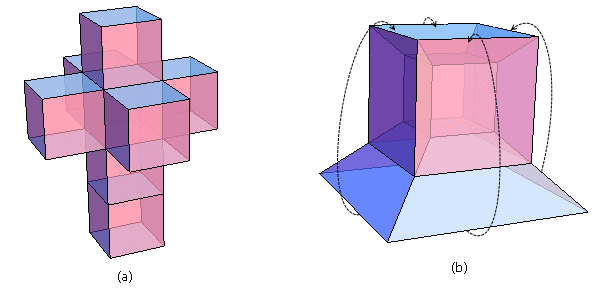
现在我告诉你，四维立方体是由8个大小相同的三维立方体组成，其展开图如图(a)。图(b)是粘合出来的四维盒子，还差一个盖子没有盖。这些看起来像棱台的东西其实都是根正苗红的正方体，只是由于它们在四维空间中位置不同，发生了透视。
把盖子盖上后，我们就看到了传说中的四维立方体，这个图形相信很多网友已经很熟悉了。图上有一大一小两个标准模样的立方体，这是第四维度上位置不同但都正对我们的两个“三维面”。其它棱台其实都是正方体，只是看上去因透视而变形。四维立方体可以看作是三维立方体的移动轨迹，因此画一个四维立方体很简单：画两个三维立方体，然后连接对应顶点即可。观察四维立方体的旋转，你会看到里面的小立方体穿过一个面跑到了外面，而后又变成了最外面的大立方体。这一切都和二维向三维的推广是类似的。仔细观察思考，你还会发现更多可以类比的地方。
上次提到，我非常关注一个即将举办的另类编程挑战赛Time Limit Exceeded，这个比赛的得分算法很另类，它将根据你代码的总长度和特定字符的多少而定。在刚刚结束的测试赛中，有几个题目非常具有挑战性，参赛者提交的代码也是牛气冲天。
Power of 2
问题：
输入数据含有多行，每行一个正整数。对每个数，检查看它是否是2的幂，是则输出yes，不是则输出no。
你的程序不允许使用分号。
规定0也是2的幂。
得分：
S= length of code + number of whitespaces;
score = (250000)/(S^2);
样例输入：
2
3
4
5
0
样例输出：
yes
no
yes
no
yes
目前的最好结果为76分：
main(t){while(~scanf("%d",&t)&&puts(t&t-1?"no":"yes")){}}
Count 1 2 3
问题：
写一个程序，该程序运行后打印出从1到50 000的整数。
你不允许使用循环语句和跳转语句（for、while、goto）。
你不允许使用#define 。
得分：
S= length of code - number of whitespaces;
score = 11 + (500*400)/(S^2);
目前的最好结果为124分，仔细体会这段代码，非常的牛：
n;main(){n<5e4&&main(printf("%d\n",++n));}
Segmentation Fault
问题：
写一个程序，该程序运行后打印出从1到5 000 000的整数。
你不允许使用循环语句和跳转语句（for、while、goto）。
你不允许使用#define 。
得分：
S= length of code - numer of whitespaces;
score = 51 + (500*1600)/(S^2);
这道题和上道题的区别就是：不加改进的递归会导致堆栈溢出。
目前的最好结果为234分，仔细观察这段代码，看他是怎样避免堆栈溢出的：
j;main(i){i>1e5||printf("%d\n",++j)+main(i+1);i<2&j<5e6&&main(1);}
创意C/C++编程挑战赛Time Limit Exceeded结束，题目果然非常有创意。大家可以在这里看到比赛题目和获胜选手的代码。其中两道题很有意思，我特别喜欢。
一道叫做Compile Error的题目要求你写一个叫做multiply的类，里面包含一个mult(int a,int b)的函数，该函数用于打印出a和b的乘积。代码中不允许出现空格、“/”和“#define”。
第一个问题就是，定义一个类的语句是class multiply{...}，这个空格要怎么避免？只要你知道typedef int foo也可以写成int typedef foo，我们就可以利用typedef来消除空格，把类的定义写成class{...}typedef multiply。但这下后面又冒出一个空格来，这个空格怎么消呢？一个巧妙的方法就是利用int typedef foo,bar的语句，把类定义语句写成class{...}typedef*foo,multiply，其中*foo是一个不会用到的类型，但是它帮助我们奇迹般地消除了一个空格。巧妙利用星号可以消除很多空格，例如我们在定义mult函数时就可以写成void*mult(...){...}。最后一个难题就是，定义函数mult(int a,int b)，参数表里面的两个空格怎么办？其实办法依然很多。不少网友都用到了typeof，这样便可以把int a写成typeof(int)a了。完整的类定义如下：
class{public:void*mult(typeof(int)a,typeof(int)b){cout<<a*b<<endl;return(0);}}typedef*m,multiply;
在gcc下，即使警告全开，下面这个程序编译时也一声不吱。
#include <iostream>
using namespace std;
class{public:void*mult(typeof(int)a,typeof(int)b){cout<<a*b<<endl;return(0);}}typedef*m,multiply;
int main()
{
multiply foo;
foo.mult(23,67);
}
另一个牛题目是Print 'D Penguin，要求你写一个打印企鹅ASCII Art的程序，程序的输出结果必须和这个文件一模一样，代码越短越好。最牛的代码有点让人摸不着头脑：
main(i,z,n){for(;z="_2���?��T���G�T��J��T��N�T��P�T�Qp�T�:�?�@�T��9��<��?T��9�8č;�9č?T��9�:�;�;��>T��9��9�;�Č9��?T�9��9�Ď?T�9�����?T��8�����@�T��9�먎AT��9�稐�A�T��9��㨓�A�T��;��@�T��;��@�T��<�A�T�����⩗��C�T�=���CT��;ਗ�C�T��<���CT�;ਧ��CT�;�ġ�C�T���=���C�T�?���D�T�?���D�T���=����C�T���Č9�ħ���D�T��Ĩ9�ė���B��T���Ĩ;ħ�?���T��Ĩ<��Ĩ�9Ĩ��T��Ĩ;�Ģ�ĩ�T���Ĩ9ਠĨ��T��Ĩ9����T���Č9���;��T��Ĩ:œ��>��T���N��T���N��T����=��A���T����騣2���T"[i++]&255;)for(n=z%28;putchar(" `x\nX '.:_"[z/28]),n--;);}
这个代码实质上是将整个图片压缩为了一个字符串。由于图片中连续字符出奇的多，我们便想到把“n个字符c”编码为一个字节。字符串的每一个字节取值都是0到255，而图片中只有10种字符（用0到9编号），因此一个字节最多可以表示出255/9=28个连续的相同字符。对于每一个0到255的数，令字符c等于它除以28的商所对应的字符，令n等于它除以28的余数，然后程序打印出n个连续的字符c出来。例如，106=3*28+22，它就代表了22个连续的3号字符。一个麻烦问题是，9*28已经等于252了，因此你最多只能处理连续的三个9号字符。不过没关系，令9号字符为“_”就行了，这是该图片中出现次数最少的字符，而且每次它都是单独出现的。
昨天晚上躺在床上发呆，想了几则数学字谜。下面每个式子都对应一个英文单词，例如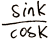
的意思就是tank。
你能猜出多少个来呢？
1. 
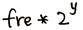
2. 
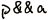
3. 
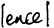
4. 
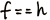
5. 
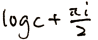
6. 
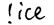
7. 
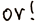
8. 
9. 
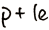
10. 
我对各种违背直觉的函数构造特别有兴趣，看看这里你就知道我对这些特殊函数有多痴迷了。因此，当我发现竟然有专门收集各种特殊函数的数学书时，可以想象我的心情有多激动。我试着以“反例”为关键字在图书馆进行检索，借了一大堆实分析数学书。这些书都已经很老了，封皮烂了又烂，已经修修补补重装了两三次封皮。翻翻这些老书，不由得对老一辈的学者和作家表示由衷的崇敬；虽然文字、排版都不出彩，但书的容量极大，内容也很实在。
废话不多说了，让我们来欣赏一下书里的一些精彩篇章吧。
实数域上一个单调递增的有界可微函数f，但lim(x→±∞)f '(x)≠0
直觉上，一个单调递增的有界函数走到无穷远的地方一定是“平”的，而事实上却并非如此。我们能构造这样一个函数，它是R上的递增有界函数，但无穷远处的导数并不等于0。
对所有非负整数n，定义f(n)=1 - 1/2^n。接下来，用下面的方式把函数扩张到全体非负实数：对区间(n, n+1)，用一条光滑的、递增的、导数由0变成1再变成0的函数来连接f(n)和f(n+1)（例如正弦函数的一个完整递增区间缩小至原大小的1/2^(n+2)再加上两根分别等于f(n)和f(n+1)的常函数）。
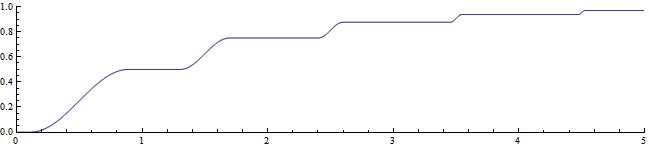
再令f(-x)=-f(x)。则这个函数是R上的一个单调递增的有界函数，但导数的极限显然不为0。事实上，这个函数的导数在无穷远处根本就没有极限，因为不管走到多远导数总能取满从0到1的所有值。
如果把问题的条件改为“严格递增”呢？对于严格递增的有界函数，无穷远处的导数也不见得为0，构造一个反例很简单，只需要在刚才那个函数上面加上一个严格单增的有界函数即可，如令g(x)=f(x)+1-1/2^n。显然，g(x)仍然单调有界，且g'(x)=f'(x) + ln(2)/2^n，其极限仍然不为0。
函数f在x0的任意小的邻域内都无界，但x→x0时f(x)并不趋于无穷大
f(x)=|cos(1/x) / x|满足要求。无论对于多大的正数N，总存在一个充分接近0的点使得f(x)>N。例如，取x=1/(nπ)，则f(x)=|1/x|=nπ，上述结论显然。
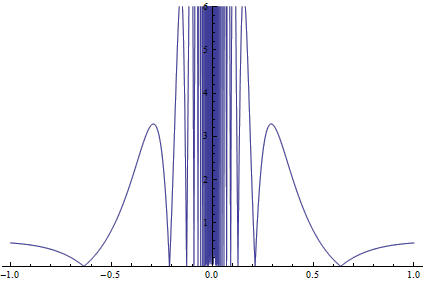
有趣的是，如果取x=1/((n+1/2) π)，则当n→∞时x→0，且f(x)→0。这说明，x趋于0时f(x)并不趋于无穷大。
f(x)→∞，不见得有f '(x)→∞
与上例比较类似。考虑(0,1)上的函数f(x)=1/x + cos(1/x)，显然lim(x→0+) f(x)=+∞ 。但f '(x)=(sin(1/x)-1)/x^2，若令x=1/(2n+1/2)π，当n→∞时f '(x)=0，这说明f '(x)→∞是不成立的。
处处有限而又处处局部无界的函数
定义函数f(x)=0 (当x为无理数)， f(x)=n (当x为有理数且可表示为既约分数m/n)。这个函数在每一点上都有意义，每一个f(x)都是有限的；但在任意小的区间内，你能找到分母任意大的既约分数，因此函数在任意小的一个区间上都是无界的。
二元函数f(x,y)在原点处不连续，但在任意一条通过原点的直线上都是连续的
定义函数f(x,y)=x^2/y，当y>0且x^2/y≤1时；f(x,y)=y/x^2，当y>0且x^2/y≥1时；当y=0时f(x,y)=0。再令f(x,-y)=f(x,y)。
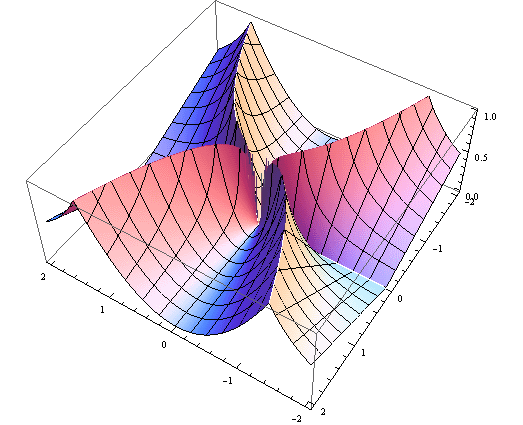
任意接近(0,0)的地方都存在形如(a, a^2)的点，相应的函数值为1，因此函数在原点间断；可是，取任意一条过原点的直线y=mx，当|x|充分小时必有x^2/y≤1，此时|f(x,y)|=|x^2/y|=|x/m|，函数在原点处连续。
小学时经常在计算器上面按12345679这个神秘的8位数。这个数牛就牛在，它乘以9的结果正好等于111111111。你可以在计算器上输好12345679，然后问MM“你的幸运数字是多少”；如果她说“7”，你就在计算器上按“乘以63”，计算器上将会显示出清一色的7字，看上去无比壮观。
假如123456789×9=1111111111的话，我倒不会觉得奇怪。网上流行过一个火星帖子，写了一大堆诸如111111111 * 111111111 = 12345678987654321的式子来展示数学之美，以至于大家会认为123456789×9的结果也一定是一串很有规律的数字。因此，如果我不在这里说一句123456789×9其实并不等于1111111111的话，估计很多人都发现不了问题。事实上，123456789×9=1111111101，偏偏就差一个“1”。而怪就怪在，去掉被除数中的数字“8”，偏偏又有了12345679×9=111111111，一个极其别扭的算式反而得到了完美的结果。不要让你的直觉被数学之美所蒙蔽，数学上有大量出人意料的、看上去很不对称的结论。
为什么偏偏要少一个“8”呢？难道这真的是算术中的一个不可抹去的疤痕？我们急需要寻求一个解释，填补上算术中的这个不和谐的“漏洞”。一种解释是，我们看到了123456789×9=1111111101并不美观，想要对其进行改造，进而得到(123456789+1)*9 = 1111111101+9 = 1111111110，于是(123456789+1)*9/10 = 12345679*9 = 111111111。用这种办法的确可以解释“迷失的8”，不过这个解释并不漂亮。为了寻求一个更好的解释，我们来看一看111111111和9的关系。
或许大家都知道，利用等比数列求和，我们可以把任一循环小数还原为分数。111...11和9之间有一个非常精妙的联系：1/9 = 0.111... 。换句话说，1000000000/9取整之后就应该等于111111111。而这个神秘的12345679，就应该是1000000000/81取整后的结果了。1/81到底等于多少呢？拿精度稍微高一点的计算器一算，我们发现1/81 = 0.01234567901234... 。原来，12345679的秘密全在1/81里面，12345679*9=111111111其实相当于是拿1/81乘以9，取得了1/9的小数部分。
现在余留的问题就是，为什么1/81的前面几位是.012345679呢？仔细观察这个小数，你会发现整个小数的循环节就是012345679，偏偏就少一个“8”。这到底是为什么呢？
为了解释一种反常的数学现象，一个有趣的思路就是，“如果不是这样，你觉得又该是怎样呢？”理想中，这种有悖于数学之美的事情是不应该发生的，1/81要是等于0.01234567890123456789...就好了，或者更牛B一点的，有没有可能等于0.0123456789101112131415...？哦，这个好像太夸张了，后面这个小数明显是一个无限不循环小数，不可能和一个有理数相等。不过呢，Σn/10^(n+1)倒是有可能的。想到这一点，我们最初的谜题迎刃而解！
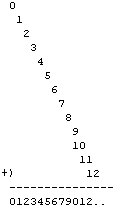
原来，“迷失的8”并不是一个算术上的瑕疵。或许1/81的小数部分本来就应该是123456789..，接下去的一个数应该是10，但它应该占据两个数的位置，而留给它的原本只有一个数位。于是乎，数字10中的个位“0”与“9”的后面一位对齐，而十位“1”则加到了“9”身上并产生了进位，得到了123456790的结果，产生了“迷失的8”这一错觉。而后，刚才10的个位“0”又加上了紧随其后的11的十位，11的个位又和12的十位拼成了“2”，如此反复，使得整个小数部分不断地重复012345679这一循环。
1/81=Σn/10^(n+1)这一猜测似乎很合理，究竟对不对呢？这和81又有什么关系呢？只需要注意到1/81=(1/9)*(1/9)，联想前面我们讲过的东西，我们就得到了一个虽然不严密但是颇有启发性的推理。111*111=12321，是因为111*111相当于把111错位写成三行后加起来；类似地，前面提到的极端情形111111111 * 111111111 = 12345678987654321也是如此。那么，如果10个1乘以10个1呢？如果无穷个“1”乘以无穷个“1”呢？当我们计算1/9的平方时，我们实际上在做的正是用无穷多个1去乘以无穷多个1，而乘式的第n+1列里恰有n个“1”，它们加起来并产生适当的进位后就得到了0.0123456790123... 。
循环小数与整数之间存在着许多微妙的关系。很多时候，利用小数展开我们能解决一些无从下手的算术题目。小学奥数中有一道题目我印象极深：一个位数小于30的、以“15”打头的整数，把这个“15”移到数的末尾后，新数正好是原数的5倍。问原数是多少。很少有人能想到，解开这道题的钥匙竟然是分数和小数。假设有某个小数x的循环节就等于我们要求的数，那么
可知100x-5x=15，解得x=15/95=3/19。把3/19还原成小数，发现它的循环节是157894736842105263，问题就如此简单的解决了。
且慢，我还准备了更加精彩的数学魔术！让我们来看一看下面这套把戏：
100/9899 = 0.0101020305081321345590463 ...
牛B吧！两位两位的看，前面几个数正好形成Fibonacci数列！不过，再往后走，位数的限制迫使进位产生，打乱了原有的秩序。能让每个数的位数更长一些吗？能！请看：
1000/998999 = 0.001001002003005008013021034055089144233377610...
10000/99989999 = 0.000100010002000300050008001300210034005500890144...
100000/9999899999 = 0.00001000010000200003000050000800013000210003400055000890014400233...
这个就更加奇怪了。为什么一个简简单单的分数展开之后竟然出现了Fibonacci数列？其实，道理和前面所讲的很相似。100/9899显然是由100/(10000-100-1)得到的，让我们来看一下0.0101020305081321...乘以(10000-100-1)是否能还原成100：
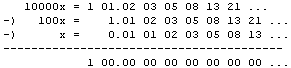
可以看到，这个“Fibonacci小数”的10000倍，减去它的100倍，再减去它自身，得到的结果正好是100，究其原因则是Fibonacci数列的递归性质。熟悉生成函数的读者猛地一拍大腿，唉呀！这不就是生成函数么！我在讲解生成函数的日志里曾经写道：
接下来我们要演示如何使用生成函数求出Fibonacci数列的通项公式。
Fibonacci数列是这样一个递推数列：f(n)=f(n-1)+f(n-2)。现在我们需要求出它的生成函数g(x)。g(x)应该是一个这样的函数：
g(x)=x+x^2+2x^3+3x^4+5x^5+8x^6+13x^7+...
等式两边同时乘以x，我们得到：
x*g(x)=x^2+x^3+2x^4+3x^5+5x^6+8x^7+...
就像我们前面说过的一样，这相当于等式右边的所有系数向右移动了一位。
现在我们把前面的式子和后面的式子相加，我们得到：
g(x)+x*g(x)=x+2x^2+3x^3+5x^4+8x^5+...
把这最后一个式子和第一个式子好好对比一下。如果第一个式子的系数往左边移动一位，然后把多余的“1”去掉，就变成了最后一个式子了。由于递推函数的性质，我们神奇地得到了：g(x)+x*g(x)=g(x)/x-1。也就是说，g(x)*x^2+g(x)*x-g(x)=-x。把左边的g(x)提出来，我们有：g(x)(x^2+x-1)=-x。于是，我们得到了g(x)=x/(1-x-x^2)。
原来，100/9899说穿了就是把x=1/100代入生成函数g(x)。
这下子就热闹了。考虑数列1, 4, 9, 16, 25, 36, ...的生成函数g(x)=x(1+x)/(1-x)^3，代入x=1/100得到g(1/100)=10100/970299，于是出现了：
10100/970299 = 0.0104091625364964 ...
当然，想要更牛B的也不难：
g(1/1000) = 1001000/997002999 = 0.001004009016025036049064081100121144169 ...
再来看看数列2, 4, 8, 16, 32, ...的生成函数g(x)=2x/(1-2x)，利用它可以产生出
g(1/100) = 1/49 = 0.0204081632 ...
或许有人会恍然大悟，原来，1/7=0.142857...也不是一个巧合。14是7的两倍，28是7的四倍，57是7的八倍加一，这都是因为它们是7乘以“2的幂序列”并产生适当进位后得到的。
重新回到我们先前讨论的话题，我们惊奇地发现，数列0, 1, 2, 3, 4, ...的生成函数为g(x)=x^2/(1-x)^2。于是：
g(1/10) = 1/81 = 0.0123456790123...
摘录几道题目。
计算1·2^2 + 2·3^2 + 3·4^2 + ... + 19·20^2
原式 = (1^3 + 2^3 + ... + 20^3) - (1^2 + 2^2 + ... + 20^2) = 44100 - 2870 = 41230
求2^x = 3^y - 1的所有正整数解
x=1时(1,1)是一个解；当x>1时，方程模4后左边永远等于0，右边则是(-1)^y - 1，可知y为偶数。令y=2z，那么有2^x = (3^z - 1)(3^z + 1)，这就要求3^z-1和3^z+1都是2的幂；但它们只相差2，因此它们只有可能是2和4，于是z=1，即原方程的另一个解为(3,2)。
圆周上有2008个点。选择两个点连成一条线，再选另外两点连一条线，这两条线段相交的概率为多少？
给定四个点，在三种连接方案中恰有一种会发生相交。取遍所有C(2008,4)种组合，相交的总情况数总是占了1/3，因此所求的概率就是1/3。
我们称一个正整数为“吉祥数”，如果它的二进制表达中有偶数个“1”。第2009个吉祥数是多少？
注意到两个正整数2k和2k+1的二进制表达中就只有最后一位不同（一个是“0”一个是“1”）。因此，2和3里面恰有一个吉祥数，4和5里面恰有一个吉祥数……以此类推，第2009个吉祥数必然是4018和4019中的一个。验证可知，4018=(111110110010)2，它有偶数个“1”，因此4018即为答案。
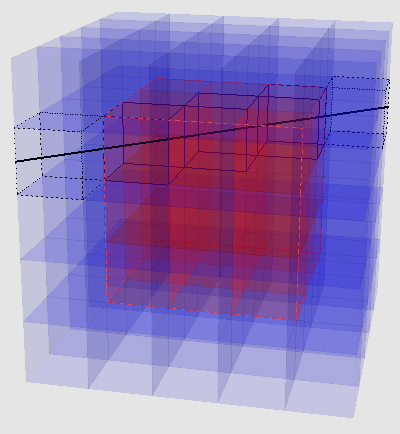
在R^n的井字棋游戏中有多少种取胜的方式？换句话说，在3*3*...*3的n维立方体棋盘中，选取三个排成一条线的小立方体有多少种可能？
给出一个我自己的解法：想象给这个立方体套一个边长为5的“外壳”，则原棋盘的每一条直线延长后都对应了外壳上的两个小立方体，外壳上的每一对位置相对的小立方体反过来也都对应着里面的棋盘中的一条直线。因此，答案为外壳上的立方体个数除以2，即(5^n-3^n)/2。
汗……图片隐藏不了……
来源：http://web.mit.edu/hmmt/www/datafiles/solutions/2009/solutions-guts-2009.pdf,
概率论并不仅仅是用来算算概率的。有些时候，概率论远比我们想象中的更强大。
考虑这样一个问题。考虑集合X上的一个集合族，集合族中的所有集合大小均为d。我们说这个集合族是可以二染色的，如果对X的元素进行适当的红蓝二着色之后，每个集合里面都包含了两种颜色的元素。例如，当d=3时，{1,2,3}, {1,2,4}, {1,3,4}, {2,3,5}就是可二染色的，把1、2染成红色，把3、4、5染成蓝色，则每个集合里都含有两种颜色。是否存在d=3的不可二染色集族呢？这样的集族当然是存在的，例如取集合{1,2,3,4,5}的全部C(5,3)个元素个数为3的子集，则无论如何染色，总会有一个集合里面的元素全是一种颜色。上述推理立即告诉我们，对于一个给定的d，一定存在一个集合个数为C(2d-1, d)的不可二染色集族。这个数目还能再少吗？我们想知道，不可二染色集族中的集合个数最少可以少到什么地步。一个极其简单的证明给出了一个下界：集族的大小一定大于2^(d-1)。当d=3时，你一辈子也不能构造一个不可二染色集族，里面只含4个集合。
为了证明这一点，不妨对X中的所有元素进行随机着色，每个元素取成红色和蓝色的概率均等。那么，一个元素个数为d的集合中，所有元素均为一种颜色的概率就应该是1/2^(d-1)。如果集族内的集合个数只有不到2^(d-1)个，那么即使“集合中是否只有一种颜色”是互相独立的，这些事件的并（至少有一个集合内只有一种颜色）的概率也不超过2^(d-1) * 1/2^(d-1) = 1，何况这些事件还不是独立的，因此存在单色集合的概率必然小于1。这个概率值小于1说明什么？这说明，“至少有一个单色集合”并不是必然事件，一定有一种染色方案使得每个元素里都含两种颜色，换句话说该集族可以被二染色。
这种证明方法奇就奇在，利用概率论进行推理得到的结果居然是一个确定的结论。Wikipedia上给出了另一个经典的概率法证明，问题仍然与染色有关。
或许大家经常听到这样一个结论：六个人在会议上握手，则存在三个两两之间都握过手，或者两两之间都没握手的人。一种更夸张的说法是，假设好友关系是双向的，那么世界上任何六个人之间或者存在三个两两都是好友的人，或者存在三个两两都不是好友的人。用图论的话说，对完全图K_6的边进行红蓝二着色，则图中一定存在一个单色的（所有边都是一种颜色的）同构于K_3的子图。K_6已经是能够满足此要求的最小完全图了，你可以尝试构造一个K_5的边二着色，使得图中不含单色的K_3子图。1930年，Frank P. Ramsey证明了，对于一个给定的r，总存在一个足够大的n，使得K_n的边二着色一定含有单色的K_r子图。这就是著名的Ramsey定理。Ramsey定理给出了n的一个上界，不过n的下界又是多少呢？1947年，Erdős的一个经典证明告诉我们，随着r的增加，n至少是指数级的增长。
为了证明这一点，我们随机给完全图K_n进行着色，每条边都有1/2的概率取红色，1/2的概率取蓝色。一个K_r子图的所有边都为红色或者都为蓝色，其概率为2·(1/2)^C(r,2)。那么对于所有C(n,r)个不同的K_r子图，单色子图个数的期望值即为C(n,r) · 2·(1/2)^C(r,2)。想想看，如果上面这个期望值小于1的话说明什么？这表明，不是所有着色方案都含有单色K_r子图，至少存在一种着色方案，它的单色K_r子图个数为0。因此，为了保证所有着色方案中都存在至少一个单色K_r子图，我们必须保证这个期望值大于等于1，也即2 · C(n,r) ≥ 2^C(r,2)。不等式右边是r(r-1)/2个2相乘的结果，不等式左边却还不及n^r，满足上述不等式至少得先保证n^r > 2^(r(r-1)/2)，这里n至少得有2^((r-1)/2)，这就足以说明n是指数级别增长的了。
很多存在性问题的证明方法都不是构造性的，它虽然证明了满足某种性质的数学对象是存在的，但并没有得出构造该数学对象的方法。利用概率进行证明往往都是非构造的，虽然证到了结论，究竟该如何寻找一个不含单色K_r子图的着色方案，这个问题直到今天仍然没有解决。
Erdős似乎是很喜欢概率法证明，最经典的一些概率证明都来源于Erdős。我们再来看一个比较复杂的例子。
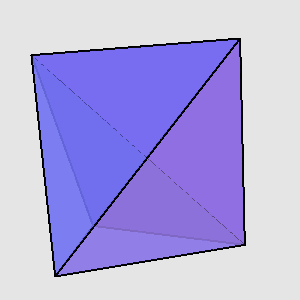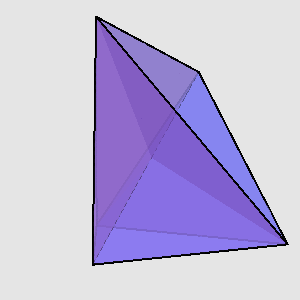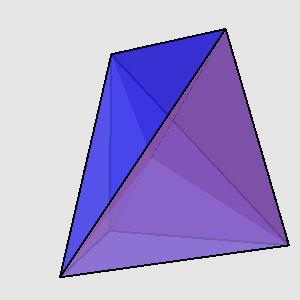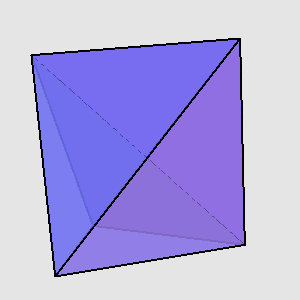
空间中的n个点确定了3·C(n,3)个角。随着n的增加，这些角不可能永远都只有锐角，总会有一个直角或者钝角冒出来。在平面上，只确定锐角的点集最多只能有三个点，摆放四个点将不可避免地产生直角或钝角。在三维空间中，五个点已经是最好的结果了（上图），可以证明六个点里无论如何都含有直角或钝角。Danzer和Grünbaum猜想：在d维空间中只含锐角的最大点集为2d-1。这个猜想始终未被证明。21年后，Paul Erdős和Zoltán Füredi推翻了这个猜想。他们用一个非构造性的证明说明，你可以从34维立方体的顶点中选取72个点，使得它们只确定出锐角。事实上，他们利用概率论证明了这样一个非概率性的事实：在d维空间中，存在一个大小为2 · [(√6/9) · (2/√3)^d]点集S⊆{0,1}^d，使得该点集所确定的角都是锐角（[x]是取x的下整的意思）。
令m=[(√6/9) · (2/√3)^d]，然后随机选取3m个0/1向量
x(1), x(2), ..., x(3m) ∈ {0,1}^d
显然，这些点所构成的角只可能是锐角或直角。向量x(i), x(j), x(k)确定一个以x(j)为顶点的直角当且仅当x(i)-x(j)与x(k)-x(j)的点积为0，换句话说对所有的坐标维l≤d都满足要么x(i)和x(j)的第l个坐标相等，要么x(k)和x(j)的第l个坐标相等。不妨把x(i)的第l个坐标记为x(i)[l]，则上述条件就可以写成x(i)[l]=x(j)[l]或x(k)[l]=x(j)[l]。我们把满足该条件的三元组(i,j,k)叫做一个“问题组”。注意，我们随机取向量时有可能取到重复的，当发生x(i)=x(j)或者x(k)=x(j)时，对应的角并不存在，但它显然也属于一个问题组。
在某一坐标l上，x(j)[l]既不等于x(i)[l]也不等于x(k)[l]只有两种情况，既x(i)[l]=x(k)[l]=0且x(j)[l]=1，以及x(i)[l]=x(k)[l]=1且x(j)[l]=0。这占了所有8种情况的1/4。由于所有向量的所有坐标都是独立选取的，因此三个向量形成问题组的概率就应该是(3/4)^d。空间中的n个点确定了3 · C(n,3)个角，因此问题组个数的期望值就应该是3 · C(3m,3) · (3/4)^d。既然期望值是这么多，这说明至少存在一种向量的取法，使得问题组的个数最多只有3 · C(3m,3) · (3/4)^d。然而
3 · C(3m,3) · (3/4)^d
< 3 · (3m)^3 · (3/4)^d / 6
= m^3 · (81/6) · (3/4)^d
= m^3 · (9/√6)^2 · (√3/2)^(2d) ≤ m
也就是说，问题组的数目不超过m个。既然这样，我们就可以去掉每个三元组中的其中一个向量（一共去掉了m个向量），破坏掉仅有的问题组，使得剩下的2m个向量中不含任一问题组。这就是一个大小为2 · [(√6/9) · (2/√3)^d]的只确定了锐角的点集。
这个模板是英文的,需要自己修改下以便支持中文.
按照ctex论坛上zpxing提供的方法:
原地址:http://bbs.ctex.org/viewthread.php?tid=33119&extra=page%3D1
模板文件下载: ftp://ftp.ctex.org/CTAN/macros/latex/contrib/moderncv.zip据英国《每日邮报》报道,英国一家皮肤癌慈善机构在网上创立了一项“透过计算机屏幕送紫外线”的活动,许诺通过计算机屏幕让那些热衷晒太阳的人,在家中接收紫外线光.这一创意吸引了上百万的点击,但这些网友很快就发现被忽悠了,当用户点击进入免费5分钟试用页面后,屏幕上就会出现一行“别傻了--紫外线会 杀死你”的警示.其实,这是推广一项皮肤癌慈善计划.
当用户点击进入免费5分钟试用页面后,屏幕上就会出现一行“别傻了--紫外线会杀死你”的警示.已吸引了百万计的点击率.
这个愚人网站于两月前创立,旨在警告公众,皮肤癌正以每天5个人的速度杀害英国人.网站向访问者展示有关皮肤癌的图例和相片,并提供连接让访问者将这个“愚人晒黑服务”传给其它朋友.
制作网站的克利福德皮肤癌慈善机构(简称Skcin)表示,网站的建立取得很大成功,极具说服力.
据悉,克利福德皮肤癌慈善机构是由因黑素瘤癌症病逝的克利福德的亲友创办的.
和谐社会，大行关键字过滤之风，甚至是“和谐”二字本身。被不幸删除或变××的称之为“被和谐了”或“被和谐掉了”。人民群众的智慧是无限的，且看文字进化过程：和谐——>河蟹——>水产
以后看到水产知道是什么了吧？别说我没教你。
如果还有别的解释方法，也提供一些吧。
以前CB曾报道过Google定居到Twitter上，而Google在Twitter发送的是一大串0和1组成的2进制代码，如果Apple也在Twitter上定居了，目前尚未公布任何消息。
已经确认世界上最大的SNS网站Facebook禁止了世界上最大的BT Tracker海盗湾的地址登记到个人资料.
同时,“分享在Facebook”按钮功能也已经不能分享海盗湾的地址,即使是合法性内容照样无法被展示出来,这意味着海盗湾已经被Facebook彻底封杀,理由是“已被报告为滥用”.
博文
所有评论
